The square root of 2, also known as Pythagoras' constant, often denoted by

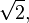
is the positive real number that, when multiplied by itself, gives the number 2. Its numerical value approximated to 65 decimal places (sequence A002193 in OEIS) is:
1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799.
The square root of 2 was probably the first known irrational number. Geometrically, it is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. On basic calculators with no square root function, the quick approximation for the square root of two is better than the quick approximation for pi, probably the most widely known irrational number.
The silver ratio is


History
There are a number of algorithms for approximating the square root of 2, which in expressions as a ratio of integers or as a decimal can only be approximated. The most common algorithm for this, one used as a basis in many computers and calculators, is the Babylonian method
Among mathematical constants with nonrepeating decimal expansions, only π has been calculated more accurately. [4]

Computation algorithm

Proofs of irrationality
One proof of the number's irrationality is the following proof by infinite descent. It is also a proof by contradiction, which means the proposition is proved by assuming that the opposite of the proposition is true and showing that this assumption is false, which means that the proposition must be true.
QED Since there is a contradiction, the assumption (1) that √2 is a rational number must be false. The opposite is proven: √2 is irrational.
This proof can be generalized to show that any root of any natural number is either a natural number or irrational.

Assume that √2 is a rational number, meaning that there exists an integer a and an integer b such that a / b = √2.
Then √2 can be written as an irreducible fraction (the fraction is reduced as much as possible) a / b such that a and b are coprime integers and (a / b) is also even which means that b is even because odd integers have odd squares.
By (5) and (8) a and b are both even, which contradicts that a / b is irreducible as stated in (2). Proof by infinite descent
An alternative proof uses the same approach with the unique factorization theorem:

Assume that √2 is a rational number, meaning that there exists an integer a and an integer b such that a / b = √2.
Then √2 can be written as an irreducible fraction (the fraction is reduced as much as possible) a / b such that a and b are coprime integers and (a / b).
This states that a prime factorization with an even power of 2 (2x) is equal to one with an odd power of 2 (2y+1). But this contradicts the unique factorization theorem. Therefore the original statement must be false. Proof by unique factorization
Another reductio ad absurdum showing that √2 is irrational is less well-known. It is also an example of proof by infinite descent. It makes use of classic compass and straightedge construction, proving the theorem by a method similar to that employed by ancient Greek geometers.
Let ABC be a right isosceles triangle with hypotenuse length m and legs n. By the Pythagorean theorem, m/n = √2. Suppose m and n are integers. Let m:n be a ratio given in its lowest terms.
Draw the arcs BD and CE with centre A. Join DE. It follows that AB = AD, AC = AE and the ∠BAC and ∠DAE coincide. Therefore the triangles ABC and ADE are congruent by SAS.
Since ∠EBF is a right angle and ∠BEF is half a right angle, BEF is also a right isosceles triangle. Hence BE = m − n implies BF = m − n. By symmetry, DF = m − n, and FDC is also a right isosceles triangle. It also follows that FC = n − (m − n) = 2n − m.
Hence we have an even smaller right isosceles triangle, with hypotenuse length 2n − m and legs m − n. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m:n is in lowest terms. Therefore m and n cannot be both integers, hence √2 is irrational.

Properties of the square root of two
The identity cos(π/4) = sin(π/4) = √2/2, along with the infinite product representations for the sine and cosine, leads to products such as

and

or equivalently,

The number can also be expressed by taking the Taylor series of a trigonometric function. For example, the series for cos(π/4) gives

The Taylor series of √(1+x) with x = 1 gives

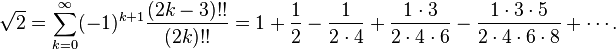
The convergence of this series can be accelerated with an Euler transform, producing

It is not known whether √2 can be represented with a BBP-type formula. BBP-type formulas are known for π√2 and √2 ln(1+√2), however. [5]

Series and product representations
The square root of two has the following continued fraction representation:


See also