In probability theory the expected value (or mathematical expectation, or mean) of a discrete random variable is the sum of the probability of each possible outcome of the experiment multiplied by the outcome value (or payoff). Thus, it represents the average amount one "expects" as the outcome of the random trial when identical odds are repeated many times. Note that the value itself may not be expected in the general sense - the "expected value" itself may be unlikely or even impossible.
For example, the expected value from the roll of an ordinary six-sided die is 3.5, found by,
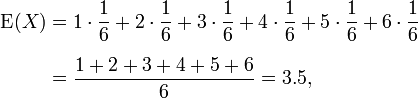which is not one of the possible outcomes.
A common application of expected value is in gambling. For example, an American roulette wheel has 38 equally likely outcomes. A winning bet placed on a single number pays 35-to-1 (this means that you are paid 35 times your bet and your bet is returned, so you get 36 times your bet). So considering all 38 possible outcomes, the expected value of the profit resulting from a $1 bet on a single number is:

which is about −$0.0526. Therefore one expects, on average, to lose over five cents for every dollar bet, and the expected value of a one dollar bet is $0.9474. In gambling or betting, a game or situation in which the expected value of the profit for the player is zero (no net gain nor loss) is commonly called a "fair game."

Mathematical definition
And so on.

When one speaks of the "expected price", one means the expected value of a random variable that is a price.
When one speaks of the "expected height", one means the expected value of a random variable that is a height.
When one speaks of the "expected number of attempts needed to get one successful attempt," one might conservatively approximate it as the reciprocal of the probability of success for such an attempt. Conventional terminology

Properties
Expected value of a constant is equal to that constant or If c is a constant, E(c) = c

Constants
If X and Y are random variables so that almost surely, then .

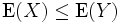Monotonicity
The expected value operator (or expectation operator) is linear in the sense that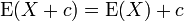



Combining the results from previous three equations, we can see that -


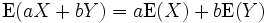
for any two random variables X and Y (which need to be defined on the same probability space) and any real numbers a and b.

Linearity

Iterated expectation
For any two discrete random variables X,Y one may define the conditional expectation:

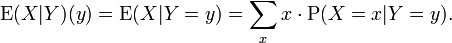
which means that is a function on y.
Then the expectation of X satisfies

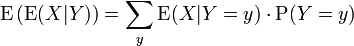
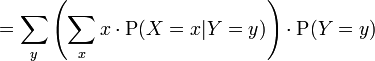
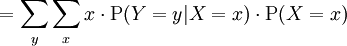
Hence, the following equation holds:

The right hand side of this equation is referred to as the iterated expectation and is also sometimes called the tower rule. This proposition is treated in law of total expectation.

Iterated expectation for discrete random variables
In the continuous case, the results are completely analogous. The definition of conditional expectation would use inequalities, density functions, and integrals to replace equalities, mass functions, and summations, respectively. However, the main result still holds:


Iterated expectation for continuous random variables
If a random variable X is always less than or equal to another random variable Y, the expectation of X is less than or equal to that of Y:
If , then .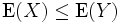
In particular, since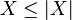 and , the absolute value of expectation of a random variable is less or equal to the expectation of its absolute value:


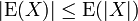
Inequality
The following formula holds for any nonnegative real-valued random variable X (such that ), and positive real number α:


Representation
In general, the expected value operator is not multiplicative, i.e.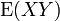 is not necessarily equal to 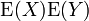. If multiplicativity occurs, the X and Y variables are said to be uncorrelated (independent variables are a notable case of uncorrelated variables). The lack of multiplicativity gives rise to study of covariance and correlation.

Non-multiplicativity
In general, the expectation operator and functions of random variables do not commute; that is

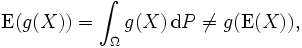
A notable inequality concerning this topic is Jensen's inequality, involving expected values of convex (or concave) functions.

Uses and applications of the expected value
If X is an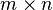 matrix, then the expected value of the matrix is defined as the matrix of expected values:

This is utilized in covariance matrices.

Computation

Conditional expectation;
An inequality on location and scale parameters;
Expected value is also a key concept in economics and finance;
The general term expectation;
Pascal's Wager;
Moment (mathematics);
Expectation value (quantum mechanics).