Pi or
π is the
ratio of a
circle's
circumference to its
diameter in
Euclidean geometry, approximately 3.14159. Pi is a
mathematical constant and a
transcendental (and therefore
irrational)
real number, with many uses in
mathematics,
physics, and
engineering. It is also known as
Archimedes' constant (not to be confused with an
Archimedes number) and as
Ludolph's number.
The letter π In
Euclidean plane geometry, π is defined as the
ratio of a
circle's
circumference to its
diameter:

Note that the ratio The formulæ below illustrate other (equivalent) definitions.
Definition The numerical value of π
truncated to 50
decimal places is:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
See the links below and those at sequence A000796 in OEIS for more digits. While the value of pi has been computed to billions of digits, practical science and engineering will rarely require more than 10 decimal places. As an example, computing the circumference of the
Earth's
equator from its radius using only 10 decimal places of pi yields an error of less than 0.2
millimeters. A value truncated to 39 decimal places is sufficient to compute the circumference of the
visible universe to a precision comparable to the size of a
hydrogen atom.
Most circular objects worthy of physical study, particularly on the scale of planetary radii, have imperfections and
eccentricities which account for a greater error in calculation than would be yielded by calculations using approximations of pi. The exact value of π has an
infinite decimal expansion: its decimal expansion never ends and does not
repeat, since π is an
irrational number (and indeed, a
transcendental number). This infinite sequence of digits has fascinated mathematicians and laymen alike, and much effort over the last few centuries has been put into computing more digits and investigating the number's properties. Despite much analytical work, and
supercomputer calculations that have determined over 1
trillion digits of π, no simple pattern in the digits has ever been found. Digits of π are available on many web pages, and there is
software for calculating π to billions of digits on any
personal computer.
See history of numerical approximations of π.
Numerical value Main article: Computing π Calculating π The constant π is an
irrational number; that is, it cannot be written as the ratio of two
integers. This was proven in
1761 by
Johann Heinrich Lambert. See
Proof that π is irrational for an elementary proof due to
Ivan Niven.
Furthermore, π is also
transcendental, as was proven by
Ferdinand von Lindemann in
1882. This means that there is no
polynomial with
rational coefficients of which π is a
root. An important consequence of the transcendence of π is the fact that it is not
constructible. Because the coordinates of all points that can be constructed with
compass and straightedge are constructible numbers, it is impossible to
square the circle: that is, it is impossible to construct, using compass and straightedge alone, a square whose area is equal to the area of a given circle.
History Often
William Jones' book
A New Introduction to Mathematics from
1706 is cited as the first text where the
Greek letter π was used for this constant, but this notation became particularly popular after
Leonhard Euler adopted it in 1737 (
cf History of π).
Use of the symbol π Main article: History of numerical approximations of π Early approximations Main article: History of numerical approximations of π Numerical approximations Formulae The constant
π appears in many formulæ in
geometry involving
circles and
spheres.
All of these formulae are a consequence of the formula for circumference. For example, the area of a circle of radius R can be accumulated by summing
annuli of infinitesimal width using the integral

. The others concern a surface or
solid of revolution.
Also, the
angle measure of 180° (
degrees) is equal to
π radians.
Geometry Many formulas in
analysis contain
π, including
infinite series (and
infinite product) representations,
integrals, and so-called
special functions.



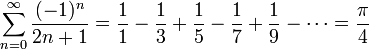








where the nth factor is the 2/2:
Stirling's approximation
Euler's identity (called by Richard Feynman "the most remarkable formula in mathematics")
A property of Euler's totient function (see also Farey sequence)
An application of the residue theorem Analysis
Some results from number theory:
In the above three statements, "probability", "average", and "random" are taken in a limiting sense, i.e. we consider the probability for the set of integers {1, 2, 3,…, N}, and then take the limit as N approaches infinity.
The theory of elliptic curves and complex multiplication derives the approximation

which is valid to about 30 digits.
The probability that two randomly chosen integers are coprime is . Number theory
Consider the recurrence relation
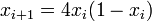
Then for almost every initial value x0 in the unit interval [0,1],
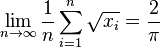
This recurrence relation is the logistic map with parameter r = 4, known from dynamical systems theory. See also: ergodic theory.
 Dynamical systems and ergodic theory
Dynamical systems and ergodic theory
The number π appears routinely in equations describing fundamental principles of the Universe, due in no small part to its relationship to the nature of the circle and, correspondingly, spherical coordinate systems.


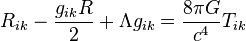

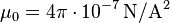
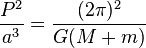
The cosmological constant:
Heisenberg's uncertainty principle:
Einstein's field equation of general relativity:
Coulomb's law for the electric force:
Magnetic permeability of free space:
Kepler's third law constant: Physics
In probability and statistics, there are many distributions whose formulæ contain π, including:
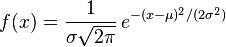
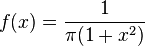
Note that since 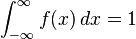 , for any pdf f(x), the above formulæ can be used to produce other integral formulae for π.
, for any pdf f(x), the above formulæ can be used to produce other integral formulae for π.
A semi-interesting empirical approximation of π is based on Buffon's needle problem. Consider dropping a needle of length L repeatedly on a surface containing parallel lines drawn S units apart (with S > L). If the needle is dropped n times and x of those times it comes to rest crossing a line (x > 0), then one may approximate π using:

[As a practical matter, this approximation is poor and converges very slowly.]
Another approximation of π is to throw points randomly into a quarter of a circle with radius 1 that is inscribed in a square of length 1. π, the area of a unit circle, is then approximated as 4×(points in the quarter circle) ÷ (total points).
probability density function (pdf) for the normal distribution with mean μ and standard deviation σ:
pdf for the (standard) Cauchy distribution: Probability and statistics
In the early years of the computer, the first expansion of π to 100,000 decimal places was computed by Maryland mathematician Dr. Daniel Shanks and his team at the United States Naval Research Laboratory (N.R.L.) in 1961.
Daniel Shanks and his team used two different power series for calculating the digits of π. For one it was known that any error would produce a value slightly high, and for the other, it was known that any error would produce a value slightly low. And hence, as long as the two series produced the same digits, there was a very high confidence that they were correct. The first 100,000 digits of π were published by the Naval Research Laboratory.
None of the formulæ given above can serve as an efficient way of approximating π. For fast calculations, one may use a formula such as Machin's:
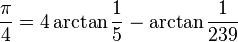
together with the Taylor series expansion of the function arctan(x). This formula is most easily verified using polar coordinates of complex numbers, starting with

Formulæ of this kind are known as Machin-like formulae.
Many other expressions for π were developed and published by Indian mathematician Srinivasa Ramanujan. He worked with mathematician Godfrey Harold Hardy in England for a number of years.
Extremely long decimal expansions of π are typically computed with the Gauss-Legendre algorithm and Borwein's algorithm; the Salamin-Brent algorithm which was invented in 1976 has also been used.
The first one million digits of π and binary or hexadecimal digit of π, without having to compute the preceding k − 1 digits. Bailey's website contains the derivation as well as implementations in various programming languages. The PiHex project computed 64-bits around the quadrillionth bit of π (which turns out to be 0).
Fabrice Bellard claims to have beaten the efficiency record set by Bailey, Borwein, and Plouffe with his formula to calculate binary digits of π [2]:
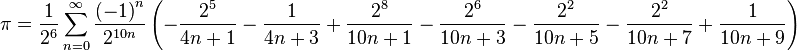
Other formulæ that have been used to compute estimates of π include:

Newton.
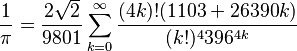
Srinivasa Ramanujan.
This converges extraordinarily rapidly. Ramanujan's work is the basis for the fastest algorithms used, as of the turn of the millennium, to calculate π.
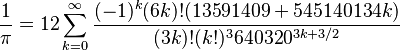
David Chudnovsky and Gregory Chudnovsky.
Efficient methods
The base 60 representation of π, correct to eight significant figures (in base 10) is:

In addition, the following expressions approximate π:

 Ramanujan claimed he had a dream in which the goddess Namagiri appeared and told him the true value of π. /113…. These approximations are the best possible rational approximations of π relative to the size of their denominators. Miscellaneous formulæ
Ramanujan claimed he had a dream in which the goddess Namagiri appeared and told him the true value of π. /113…. These approximations are the best possible rational approximations of π relative to the size of their denominators. Miscellaneous formulæ
Main article: Piphilology Memorizing digits The most pressing open question about
π is whether it is a
normal number -- whether any digit block occurs in the expansion of
π just as often as one would statistically expect if the digits had been produced completely "randomly", and that this is true in
every base, not just base 10. Current knowledge on this point is very weak; e.g., it is not even known which of the digits 0,…,9 occur infinitely often in the decimal expansion of
π.
Bailey and Crandall showed in
2000 that the existence of the above mentioned
Bailey-Borwein-Plouffe formula and similar formulae imply that the normality in base 2 of
π and various other constants can be reduced to a plausible
conjecture of
chaos theory. See Bailey's above mentioned web site for details.
It is also unknown whether
π and
e are
algebraically independent. However it is known that at least one of
πe and
π +
e is
transcendental (see
Lindemann–Weierstrass theorem).
Open questions In
non-Euclidean geometry the sum of the angles of a
triangle may be more or less than
π radians, and the ratio of a circle's circumference to its diameter may also differ from
π. This does not change the definition of
π, but it does affect many formulæ in which
π appears. So, in particular,
π is not affected by the
shape of the universe; it is not a
physical constant but a mathematical constant defined independently of any physical measurements. Nonetheless, it occurs often in physics.
For example, consider
Coulomb's law (SI units)

.
Here, 4
πr is just the surface area of sphere of radius
r. In this form, it is a convenient way of describing the inverse square relationship of the force at a distance
r from a point source. It would of course be possible to describe this law in other, but less convenient ways, or in some cases more convenient. If
Planck charge is used, it can be written as

and thus eliminate the need for
π.
Naturality List of topics related to pi Proof that π is irrational Calculus Geometry Trigonometric function Pi through experiment A simple proof that 22/7 exceeds π Feynman point comprising the 762nd through 767th decimal places of π, consisting of the digit 9 repeated six times.
Indiana Pi Bill the attempt to legislate π = 3.2
Pi Day Lucy Tuning Cadaeic Cadenza Software for calculating π on personal computers
Mathematical constants:
e and
φ Footnotes Bailey, David H., Borwein, Peter B., and Plouffe, Simon (April 1997). "On the Rapid Computation of Various Polylogarithmic Constants". Mathematics of Computation 66 (218): 903–913. Rudin, Walter [1953] (1976). Principles of mathematical analysis, 3e, McGraw-Hill. ISBN 0-07-054235-X. A new formula to compute the n'th binary digit of pi by Fabrice Bellard, retrieved March 22, 2006
Beckmann, Petr (1976). A History of π. St. Martin's Griffin. ISBN 0-312-38185-9. Jonathan Sondow,
"A faster product for pi and a new integral for ln /2," Amer. Math. Monthly 112 (2005) 729-734.
Jonathan Sondow, Problem 88, Math Horizons 5 (Sept., 1997) 32, 34
Borwein, Jonathan M.; Borwein, Peter; and Berggren, Lennart (2004).
Pi: A Source Book, Springer.
ISBN 0-387-20571-3.

 . The others concern a surface or
. The others concern a surface or 


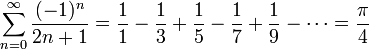









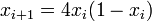
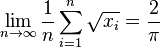
 Dynamical systems and ergodic theory
Dynamical systems and ergodic theory

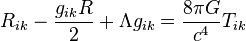

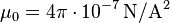
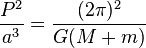
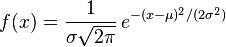
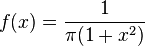
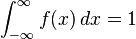 , for any pdf f(x), the above formulæ can be used to produce other integral formulae for π.
, for any pdf f(x), the above formulæ can be used to produce other integral formulae for π.
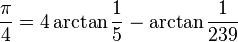

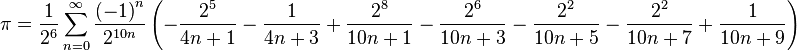

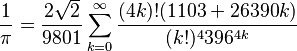
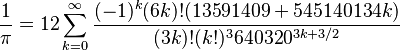



 .
.

No comments:
Post a Comment